Uma forma simples de obter a área de um triângulo qualquer conhecendo dois lados e um ângulo é através da fórmula LLA. A dedução desta fórmula é bem simples e requer os seguintes requisitos: Conhecer a identidade trigonométrica a soma de arcos - seno da diferença, fórmula elementar da área de um triângulo \(\text{Área}=\frac{\text{base} \cdot \text{altura}}{2}\).
\(\require{gensymb}\)
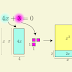
Traçando uma altura relativa à base do triângulo, \(c\), como na imagem abaixo.
O triângulo \(\triangle APC \) é retângulo, logo,
\begin{equation}
\sin\alpha = \frac{\text{cateto oposto}}{\text{hipotenusa}} = \frac{h}{b}
\label{eq:1}
\end{equation}
Então
\begin{equation}
h = b \cdot \sin\alpha
\label{eq:2}
\end{equation}
A fórmula básica para calcular a área de qualquer triângulo conhecendo a sua base e sua altura é dada por.
\begin{equation}
\text{Área}(\triangle)=\frac{\text{base} \cdot \text{altura}}{2}
\label{eq:3}
\end{equation}
Como conhecemos a base \(c\) e a altura \(h\) em \((\ref{eq:2})\) do triângulo \(\triangle ABC\), basta substituí-los em \((\ref{eq:3})\).
\begin{equation}
\text{Área}(\triangle)=\frac{c \cdot b \cdot \sin\alpha}{2}
\label{eq:4}
\end{equation}
\(\blacksquare\)
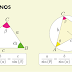
No exemplo acima o ângulo \(\alpha\) é agudo, ou seja \(\alpha \lt 90 \degree\). Será se a fórmula também funciona para ângulos abtusos (maior que \(90\degree \))? Vamos verificar.

A altura \(h\) do triângulo \(\triangle ABC\), quando \(\alpha \gt 90 \degree \), se relaciona com o ângulo \(180\degree -\alpha \). logo.
\begin{equation}
\sin(180 - \alpha) = \frac{h}{b}
\label{eq:5}
\end{equation}
\begin{equation}
h = b \cdot \sin(180 - \alpha)
\label{eq:6}
\end{equation}
Como conhecemos a identidade trigonométrica a soma de arcos - seno da diferença.
\begin{equation}
\sin(180-\alpha) = \sin 180 \cdot \cos \alpha - \sin \alpha \cdot cos 180
\label{eq:7}
\end{equation}
A saber.
\begin{equation}
\sin180 = 0
\label{eq:8}
\end{equation}
\begin{equation}
cos180 = -1
\label{eq:9}
\end{equation}
Então, substituindo \((\ref{eq:8})\) e \((\ref{eq:9})\) em \((\ref{eq:7})\), temos.
\begin{equation}
\sin(180-\alpha) = \cancel{\sin 180 \cdot \cos \alpha} - \sin \alpha \cdot (-1)
\label{eq:10}
\end{equation}
\begin{equation}
\sin(180 - \alpha) = \sin \alpha
\label{eq:11}
\end{equation}
Substituindo \((\ref{eq:11})\) em \((\ref{eq:6})\).
\begin{equation}
h = b \cdot \sin(180 - \alpha) = b \cdot \sin \alpha
\label{eq:12}
\end{equation}
\begin{equation}
h = b \cdot \sin \alpha
\label{eq:13}
\end{equation}
Como a área de um triângulo qualquer é igual a \(\frac{\text{base*altura}}{2}\), logo.
\begin{equation}
\text{Área}(\triangle)=\frac{c \cdot b \cdot \sin\alpha}{2}
\label{eq:14}
\end{equation}
Portanto, a fórmula LLA funciona para qualquer valor de alpha, \(0 \lt \alpha \lt 180 \degree \).
Outro ponto importante, as fórmulas LLA e AALL são equivalantes.

Atividade para casa :) - Demonstre que a área de um triângulo qualquer é igual a.
\begin{equation}
\text{Área}(\triangle)=\frac{b \cdot c}{2} \cdot\sin(\theta + \beta)
\label{eq:15}
\end{equation}
Lembre-se: A soma dos ângulos internos de um triângulo (na geometria euclidiana plana) é sempre igual a \(180\degree\).
Notas e referências