
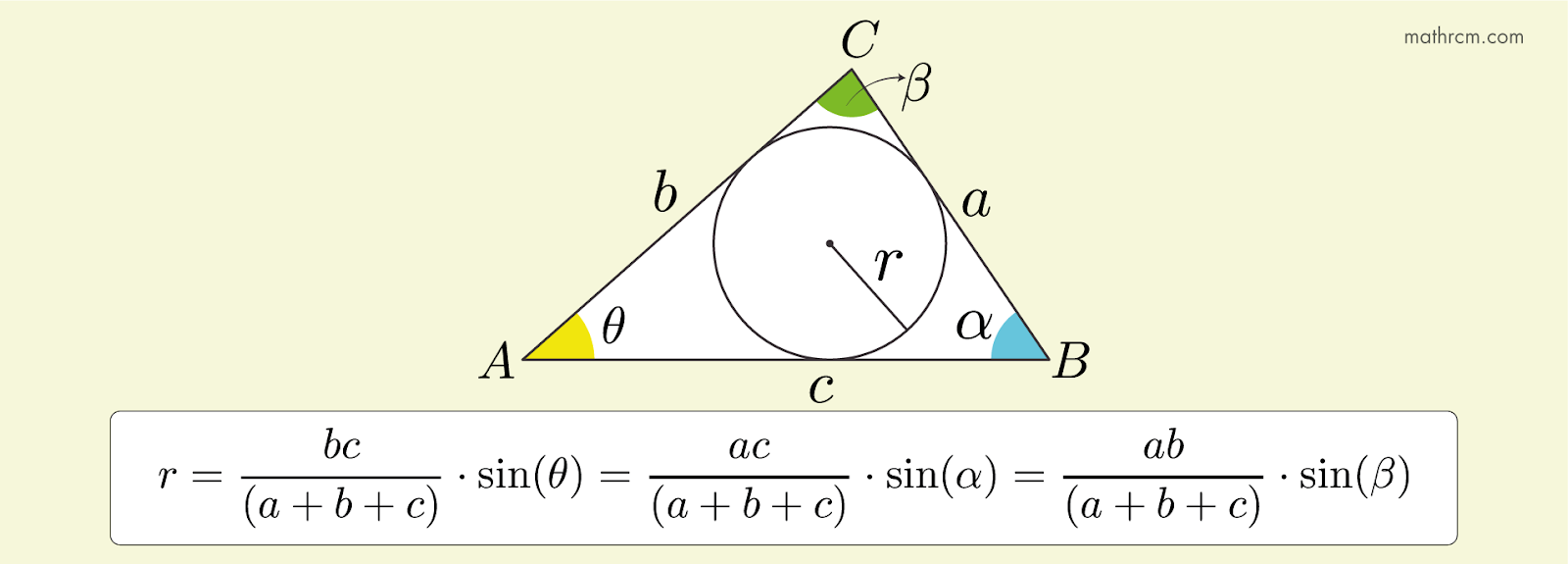
Podemos obter o comprimento do raio da circunferência inscrita, relacionado o seno de um ângulo conhecido e os lados do triângulo circunscrito.
O
radical especial presente nas alturas de um triângulo qualquer é sempre igual a um certo valor, mesmo permutando os segmentos \(a, b\) e \( c\).
\begin{equation}
x = \sqrt{4b^2c^2-(b^2+c^2-a^2)^2}=\sqrt{4a^2c^2-(a^2+c^2-b^2)^2}= \sqrt{4a^2b^2-(a^2+b^2-c^2)^2} \label{eq:raioIncentro1}
\end{equation}
\begin{equation}
x = \sqrt{(a+b+c)(a+b-c)(a+c-b)(b+c-a)} \label{eq:raioIncentro1.1.1}
\end{equation}
Esse radical especial também está presente no
comprimento do raio da circunferência inscrita.
\begin{equation}
r =\frac{\sqrt{4a^2c^2-(a^2+c^2-b^2)^2}}{2(a+b+c)} = \frac{x}{2(a+b+c)}
\label{eq:raioIncentro2}
\end{equation}
Esse radical também está presente nos senos dos ângulos.
\begin{equation}
\sin(\theta) = \frac{\sqrt{4b^2c^2-(b^2+c^2-a^2)^2}}{2bc} = \frac{x}{2bc} \label{eq:raioIncentro3}
\end{equation}
Logo,
\begin{equation}
2bc\cdot \sin(\theta) = x \label{eq:raioIncentro4}
\end{equation}
Substituindo (\(\ref{eq:raioIncentro2}\)) em (\(\ref{eq:raioIncentro4}\)), tem-se.
\begin{equation}
r = \frac{\cancel{2}bc\cdot \sin(\theta)}{\cancel{2}(a+b+c)}
\label{eq:raioIncentro5}
\end{equation}
\begin{equation}
r = \frac{bc}{(a+b+c)}\cdot \sin(\theta)
\label{eq:raioIncentro6}
\end{equation}
Analogamente, podemos repetir os passos acima para os demais ângulos.
\begin{equation}
r = \frac{bc}{(a+b+c)}\cdot \sin(\theta) = \frac{ac}{(a+b+c)}\cdot \sin(\alpha) = \frac{ab}{(a+b+c)}\cdot \sin(\beta)
\label{eq:raioIncentro7}
\end{equation}
\(\blacksquare\)
Notas e referências
Como fazer referência ao post
Rodrigo da Costa. O comprimento do raio da circunferência, inscrita em um triângulo, em função do seno de um ângulo e dos lados do triângulo. rcmath, 07/12/2023. Disponível em: < https://www.rcmath.com/2023/12/o-comprimento-do-raio-da-circunferencia-inscrita-em-funcao-do-seno-de-um-angulo-e-dos-lados-do-triangulo.html >. Acesso em: .






0 comments:
Postar um comentário