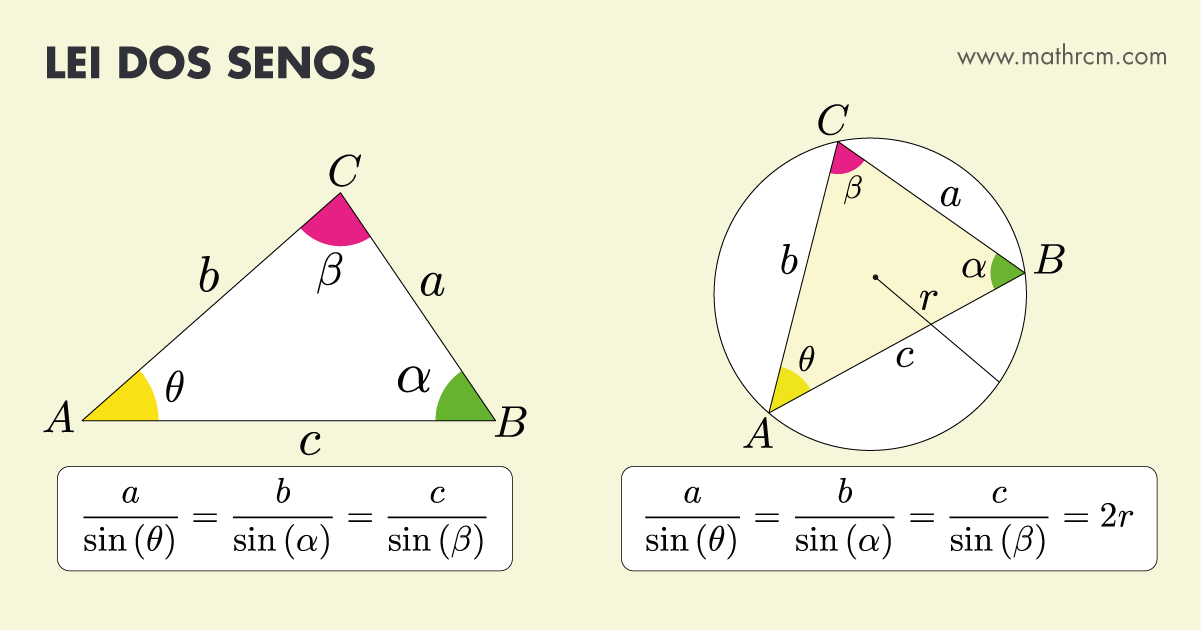
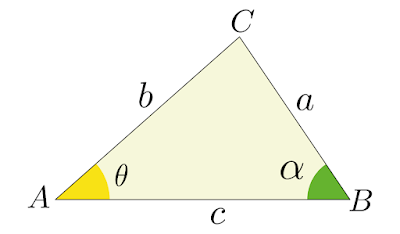
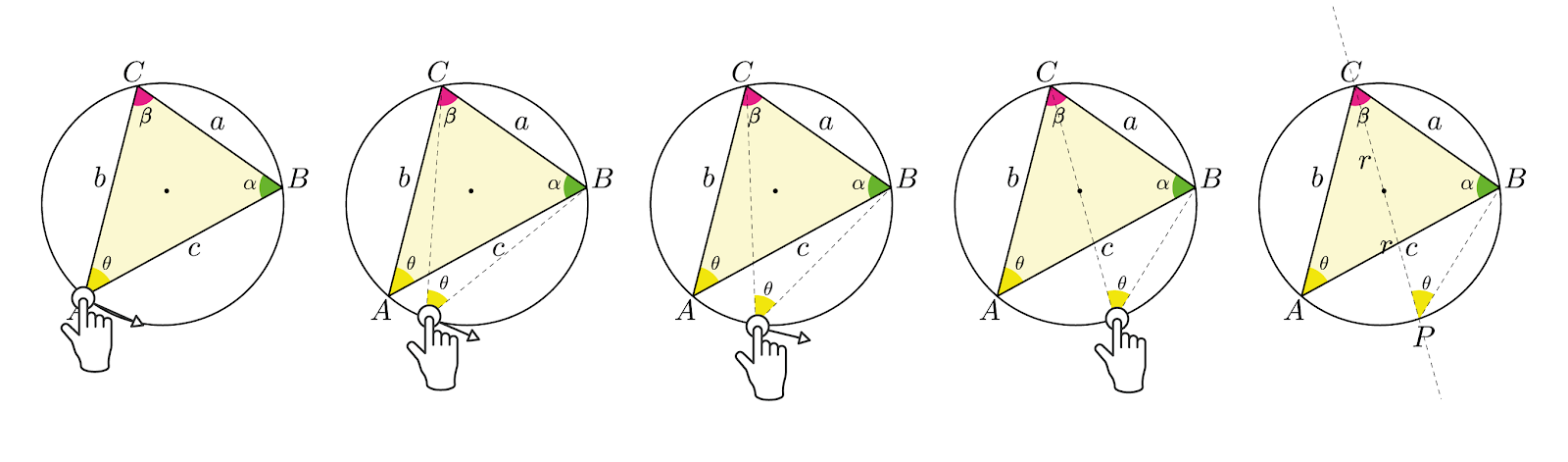
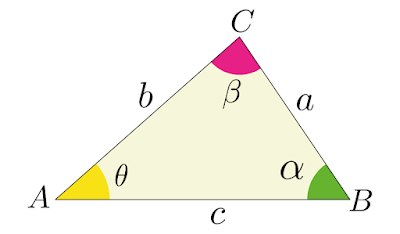
Em um triângulo qualquer, há três razões que relacionam o lado oposto a um determinado ângulo com o seno desse mesmo ângulo, sendo essas três razões proporcionais. Elas são conhecidas como a Lei dos Senos.
\(\require{gensymb}\)
\begin{equation}
\frac{a}{\sin(\theta)} = \frac{b}{\sin(\alpha)} = \frac{c}{\sin(\beta)}
\label{eq:leiDosSenos1}
\end{equation}
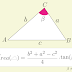
Uma forma simples de demonstrar a Lei dos senos é a partir da fórmula da área, em função do seno de um ângulo conhecido e dos dois lados adjacentes ao mesmo, de um triângulo qualquer. Na figura abaixo, a área do triângulo \(\triangle ABC\) é igual a.
\begin{equation}
A=\frac{bc}{2}\cdot \sin(\theta)
\label{eq:leiDosSenos2}
\end{equation}
Assim como,
\begin{equation}
A=\frac{ac}{2}\cdot \sin(\alpha)
\label{eq:leiDosSenos3}
\end{equation}
Como as duas áreas são iguais, basta substituir (\ref{eq:leiDosSenos2}) em (\ref{eq:leiDosSenos3}),
\begin{equation}
\frac{b\cancel{c}}{\cancel{2}}\cdot \sin(\theta)=\frac{a\cancel{c}}{\cancel{2}}\cdot \sin(\alpha)
\label{eq:leiDosSenos4}
\end{equation}
\begin{equation}
\frac{b}{\sin(\alpha)}=\frac{a}{\sin(\theta)}
\label{eq:leiDosSenos5}
\end{equation}
Igualando as áreas, tendo como referência os ângulos \(\theta\) e \(\beta\), obtemos a seguinte relação.
\begin{equation}
\frac{a}{\sin(\theta)}=\frac{c}{\sin(\beta)}
\label{eq:leiDosSenos6}
\end{equation}
Portanto,
\begin{equation}
\frac{a}{\sin(\theta)} = \frac{b}{\sin(\alpha)} = \frac{c}{\sin(\beta)}
\label{eq:leiDosSenos7}
\end{equation}
\(\blacksquare\)
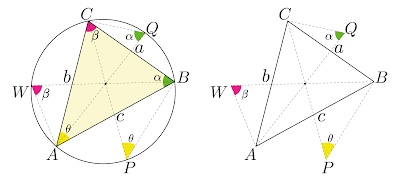
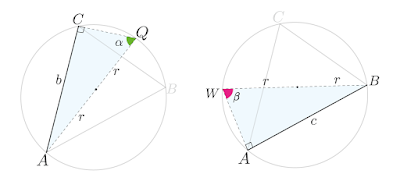
Uma outra forma de demonstrar a lei dos senos é a partir de um triângulo inscrito em uma circunferência, sendo a razão do lado oposto ao ângulo pelo seno desse mesmo ângulo proporcional a 2 vezes o raio da circunferência.
\begin{equation}
\frac{a}{\sin(\theta)} = \frac{b}{\sin(\alpha)} = \frac{c}{\sin(\beta)} = 2r
\label{eq:leiDosSenos8}
\end{equation}
Desloca-se um dos vértices do triângulo sobre a circunferência até que um dos lados do novo triângulo coincida com o diâmetro da circunferência. Observe a imagem abaixo, a mão\(^{1}\) desloca o vértice \(A\) até o ponto \(P\).
Deslocando os demais vértices.
Pelo
teorema de Tales, quando um dos lados de um triângulo inscrito coincide com o diâmetro da circunferência, o ângulo oposto ao diâmetro mede \(90\degree\).
O \(\sin(\theta)\) no triângulo \(\triangle PBC\), figura acima, é igual a.
\begin{equation}
\sin(\theta) = \frac{cateto-oposto}{hipotenusa}=\frac{a}{2r}
\label{eq:leiDosSenos9}
\end{equation}
\begin{equation}
\frac{a}{\sin(\theta)} = 2r
\label{eq:leiDosSenos10}
\end{equation}
O \(\sin(\alpha)\) e \(\sin(\beta)\) .
No triângulo \(\triangle AQC\), figura acima, o \(\sin(\alpha)\) é igual a.
\begin{equation}
\frac{b}{\sin(\alpha)} = 2r
\label{eq:leiDosSenos11}
\end{equation}
No triângulo \(\triangle ABW\), figura acima, o \(\sin(\beta)\) é igual a.
\begin{equation}
\frac{c}{\sin(\beta)} = 2r
\label{eq:leiDosSenos12}
\end{equation}
Como (\(\ref{eq:leiDosSenos10}\)), (\(\ref{eq:leiDosSenos11}\)) e (\(\ref{eq:leiDosSenos12}\)) são iguais, logo.
\begin{equation}
\frac{a}{\sin(\theta)} = \frac{b}{\sin(\alpha)} = \frac{c}{\sin(\beta)} = 2r
\label{eq:leiDosSenos13}
\end{equation}
\(\blacksquare\)
Notas e referências
- \(^{1}\) A imagem da mão foi obtida sob Licença grátis em br.freepik.com e pertence ao usuário rawpixel.com | Imagem de rawpixel.com
\(\require{gensymb}\)
\begin{equation}
\frac{a}{\sin(\theta)} = \frac{b}{\sin(\alpha)} = \frac{c}{\sin(\beta)}
\label{eq:leiDosSenos1}
\end{equation}
