\(\require{gensymb}\)
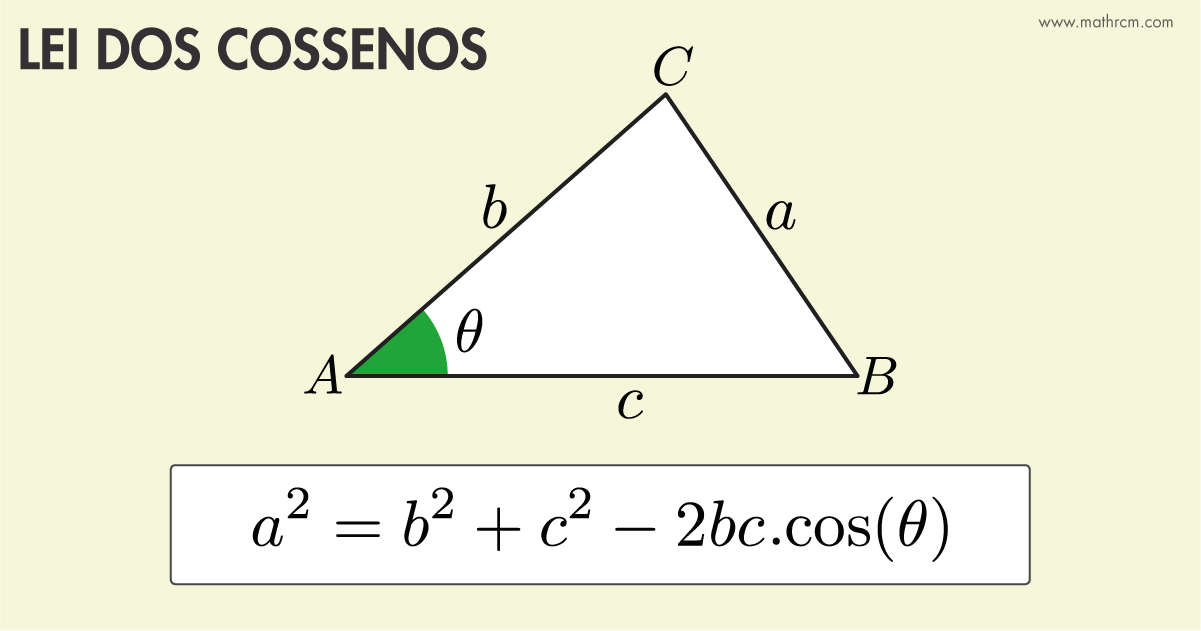
A lei dos cossenos relaciona um ângulo conhecido e os dois lados adjacente ao mesmo, para encontrar o comprimento do lado oposto ao ângulo. Na Figura (1), para encontrar o comprimento do lado \(a\), basta conhecer o ângulo \(\theta\) e os lados \(b\) e \(c\).
 |
| Figura 1 |
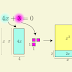
Traçando uma altura relativa a base \(c\) e aplicando Pitágoras ao triângulo \(\triangle APC\).
 |
| Figura 2 |
\begin{equation}
b^2 = h^2+(c-x)^2 \label{eq:3.10}
\end{equation}
\begin{equation}
h^2=b^2-(c-x)^2 \label{eq:3.11}
\end{equation}
\begin{equation}
h^2=b^2-c^2+2cx-x^2 \label{eq:3.12}
\end{equation}
O cosseno do ângulo \(\theta\) \(\measuredangle PAC\) do triângulo \(\triangle APC\) é igual a.
\begin{equation}
cos(\theta) = \frac{c-x}{b}
\label{eq:3.13}
\end{equation}
\begin{equation}
x = c - b\cdot cos(\theta)
\label{eq:3.14}
\end{equation}
Aplicando Pitágoras ao triângulo \(\triangle BPC\).
\begin{equation}
a^2=h^2+x^2
\label{eq:3.15}
\end{equation}
Substituindo (\ref{eq:3.12}) em (\ref{eq:3.15}).
\begin{equation}
a^2=b^2-c^2+2cx \cancel{-x^2} \cancel{+x^2}
\label{eq:3.16}
\end{equation}
\begin{equation}
a^2=b^2-c^2+2cx
\label{eq:3.17}
\end{equation}
Substituindo (\ref{eq:3.14}) em (\ref{eq:3.17}).
\begin{equation}
a^2=b^2-c^2+2c(c - b\cdot cos(\theta))
\label{eq:3.18}
\end{equation}
\begin{equation}
a^2=b^2-c^2+2c^2 - 2bc\cdot cos(\theta))
\label{eq:3.19}
\end{equation}
Portanto.
\begin{equation}
a^2=b^2+c^2 - 2bc\cdot cos(\theta)
\label{eq:3.20}
\end{equation}
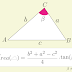
Vamos verificar se a fórmula acima é válida quando \(\theta > 90\degree\), ou seja, quando o segmento \(b\) cria uma projeção para a esquerda do vértice \(A\).
 |
| Figura 3 |
Aplicando pitágoras no triângulo \(\triangle BPC\).
\begin{equation}
a^2 = h^2 + (x+c)^2
\label{eq:3.21}
\end{equation}
Aplicando pitágoras no triângulo \(\triangle APC\).
\begin{equation}
b^2 = h^2 + x^2
\label{eq:3.22}
\end{equation}
\begin{equation}
h^2 = b^2 - x^2
\label{eq:3.23}
\end{equation}
Substituindo (\(\ref{eq:3.23}\)) em (\(\ref{eq:3.21}\)).
\begin{equation}
a^2 = b^2 - x^2 + (x+c)^2
\label{eq:3.24}
\end{equation}
\begin{equation}
a^2 = b^2 \cancel{-x^2} + \cancel{x^2}+2cx+c^2
\label{eq:3.25}
\end{equation}
\begin{equation}
a^2 = b^2+c^2+2cx
\label{eq:3.26}
\end{equation}
No \(\triangle APC\) o \(\cos(180\degree - \theta)\) é igual a.
\begin{equation}
\cos(180\degree - \theta) = \frac{x}{b}
\label{eq:3.27}
\end{equation}
\begin{equation}
x = b\cdot\cos(180\degree - \theta)
\label{eq:3.28}
\end{equation}
Aplicando a identidade trigonométrica - o cosseno da diferença de dois arcos.
\begin{equation}
\cos(180\degree - \theta) = \cos(180\degree)\cdot\cos(\theta) + \sin(180\degree)\cdot\sin(\theta)
\label{eq:3.29}
\end{equation}
Como o \(\cos(180) = -1\) e \(\sin(180) = 0\), substituindo-os em (\(\ref{eq:3.23}\)).
\begin{equation}
\cos(180\degree - \theta) = -1\cdot\cos(\theta) + \cancel{0\cdot\sin(\theta)}
\label{eq:3.30}
\end{equation}
\begin{equation}
\cos(180\degree - \theta) = -\cos(\theta)
\label{eq:3.31}
\end{equation}
Substituindo \(\ref{eq:3.31}\) em \(\ref{eq:3.28}\).
\begin{equation}
x = b\cdot(-\cos(\theta))
\label{eq:3.32}
\end{equation}
\begin{equation}
x = -b\cdot\cos(\theta)
\label{eq:3.33}
\end{equation}
Substituindo \(\ref{eq:3.33}\) em \(\ref{eq:3.26}\).
\begin{equation}
a^2 = b^2+c^2+2c(-b\cdot\cos(\theta))
\label{eq:3.34}
\end{equation}
Portanto, a lei dos cossenos é válida para qualquer valor de theta, \( 0 < \theta < 180\degree \).
\begin{equation}
a^2 = b^2+c^2-2bc\cdot\cos(\theta)
\label{eq:3.35}
\end{equation}
Além disso, podemos isolar \(\cos(\theta)\), deixando-o em função dos lados do triângulo.
\begin{equation}
cos(\theta) = \frac{b^2+c^2 -a^2}{2bc}
\label{eq:3.36}
\end{equation}
Se \(a^2 \leq b^2+c^2\), então, \(0 < \theta \leq 90\degree\), senão, \(90\degree < \theta < 180\degree\).









0 comments:
Postar um comentário