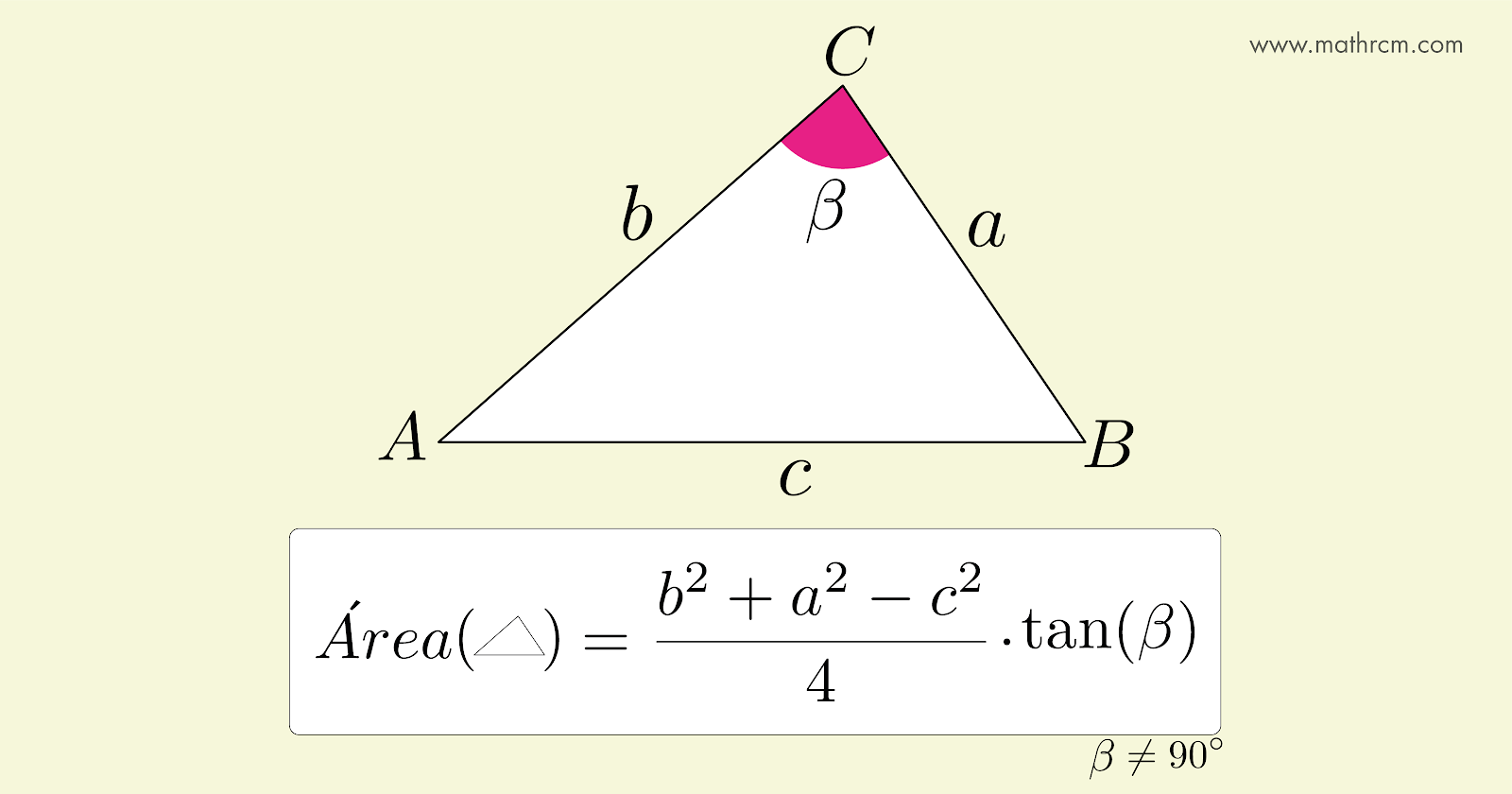
Vamos definir uma fórmula para calcular a área de um triângulo qualquer, relacionando os lados do triângulo e da tangente de um ângulo conhecido.
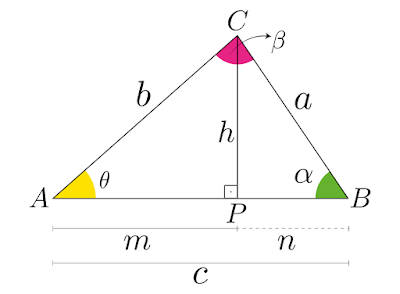
Traçando a altura relativa à base \(c\) no triângulo \(\triangle ABC\).
\(\require{gensymb}\)
Aplicando Pitágoras no triângulo \(\triangle APC\).
\begin{equation}
b^2=h^2+m^2 \label{eq:AreaTrianguloTan1}
\end{equation}
\begin{equation}
h^2=b^2-m^2 \label{eq:AreaTrianguloTan2}
\end{equation}
Aplicando Pitágoras no triângulo \(\triangle BPC\).
\begin{equation}
a^2=h^2+n^2 \label{eq:AreaTrianguloTan3}
\end{equation}
\begin{equation}
h^2=a^2-n^2 \label{eq:AreaTrianguloTan4}
\end{equation}
Substituindo \((\ref{eq:AreaTrianguloTan4})\) em \((\ref{eq:AreaTrianguloTan2})\)
\begin{equation}
a^2-n^2=b^2-m^2 \label{eq:AreaTrianguloTan5}
\end{equation}
\begin{equation}
m^2-n^2=b^2-a^2 \label{eq:AreaTrianguloTan6}
\end{equation}
Sendo \(m^2-n^2\) uma diferença de quadrados,
\begin{equation}
(m+n)(m-n)=b^2-a^2 \label{eq:AreaTrianguloTan7}
\end{equation}
Como \(m+n=c\), substituindo-o em \((\ref{eq:AreaTrianguloTan7})\),
\begin{equation}
c(m-n)=b^2-a^2 \label{eq:AreaTrianguloTan8}
\end{equation}
\begin{equation}
m-n=\frac{b^2-a^2}{c} \label{eq:AreaTrianguloTan9}
\end{equation}
\begin{equation}
m=\frac{b^2-a^2}{c}+n \label{eq:AreaTrianguloTan10}
\end{equation}
No triângulo \(\triangle BPC\), o \(\cos(\theta)\) é igual a,
\begin{equation}
\cos(\theta) = \frac{n}{a} \label{eq:AreaTrianguloTan11}
\end{equation}
No triângulo \(\triangle ABC\) o \(\cos(\theta)\), obtido pela
Lei dos cossenos, é igual a.
\begin{equation}
\cos(\theta) = \frac{a^2+c^2-b^2}{2ac} \label{eq:AreaTrianguloTan12}
\end{equation}
Substituindo \((\ref{eq:AreaTrianguloTan12})\) em \((\ref{eq:AreaTrianguloTan11})\),
\begin{equation}
\frac{n}{\cancel{a}} = \frac{a^2+c^2-b^2}{2\cancel{a}c} \label{eq:AreaTrianguloTan13}
\end{equation}
\begin{equation}
n = \frac{a^2+c^2-b^2}{2c} \label{eq:AreaTrianguloTan14}
\end{equation}
Como conhecemos o valor de \(n\) em \((\ref{eq:AreaTrianguloTan14})\) e substituindo-o em \((\ref{eq:AreaTrianguloTan10})\),
\begin{equation}
m=\frac{b^2-a^2}{c}+\frac{a^2+c^2-b^2}{2c} \label{eq:AreaTrianguloTan15}
\end{equation}
\begin{equation}
m=\frac{2b^2-2a^2+a^2+c^2-b^2}{2c} \label{eq:AreaTrianguloTan16}
\end{equation}
\begin{equation}
m=\frac{b^2+c^2-a^2}{2c} \label{eq:AreaTrianguloTan17}
\end{equation}
No triângulo \(\triangle ABC\), o ângulo \(\beta=180\degree-(\alpha+\theta)\), sendo assim, podemos aplicar a identidade trigonométrica a tangente da diferença de dois arcos em \(\beta\).
\begin{equation}
\tan(\beta) = \tan(180\degree-(\alpha+\theta)) = \frac{\tan(180\degree)-\tan(\alpha+\theta)}{1+\tan(180\degree)\cdot\tan(\alpha+\theta)}
\label{eq:AreaTrianguloTan18}
\end{equation}
Como a \( \tan(180\degree)=0 \), logo.
\begin{equation}
\tan(\beta) = \tan(180\degree-(\alpha+\theta)) = \frac{0-\tan(\alpha+\theta)}{1+0}
\label{eq:AreaTrianguloTan19}
\end{equation}
\begin{equation}
\tan(\beta) = -\tan(\alpha+\theta)
\label{eq:AreaTrianguloTan20}
\end{equation}
Resolvendo a identidade trigonométrica a tangente da soma de dois arcos: \(\tan(\alpha+\theta)\).
\begin{equation}
\tan(\alpha+\theta) = \frac{\tan(\alpha)+\tan(\theta)}{1-\tan(\alpha)\cdot \tan(\theta)}
\label{eq:AreaTrianguloTan21}
\end{equation}
Multiplicando por \(-1\) em ambos os lados da igualdade de \((\ref{eq:AreaTrianguloTan21})\),
\begin{equation}
-\tan(\alpha+\theta) = -\left( \frac{\tan(\alpha)+\tan(\theta)}{1-\tan(\alpha)\cdot \tan(\theta)}\right)
\label{eq:AreaTrianguloTan22}
\end{equation}
\begin{equation}
-\tan(\alpha+\theta) = \cancel{(-1)}\left( \frac{\tan(\alpha)+\tan(\theta)}{\cancel{(-1)}(\tan(\alpha)\cdot \tan(\theta)-1)}\right)
\label{eq:AreaTrianguloTan23}
\end{equation}
\begin{equation}
-\tan(\alpha+\theta) = \frac{\tan(\alpha)+\tan(\theta)}{\tan(\alpha)\cdot \tan(\theta)-1}
\label{eq:AreaTrianguloTan24}
\end{equation}
No triângulo \(\triangle APC\), a \(\tan(\alpha)\) é igual a,
\begin{equation}
\tan(\alpha)=\frac{h}{m}
\label{eq:AreaTrianguloTan25}
\end{equation}
No triângulo \(\triangle BPC\), a \(\tan(\theta)\) é igual a,
\begin{equation}
\tan(\theta)=\frac{h}{n}
\label{eq:AreaTrianguloTan26}
\end{equation}
Substituindo \((\ref{eq:AreaTrianguloTan25})\) e \((\ref{eq:AreaTrianguloTan26})\) em \((\ref{eq:AreaTrianguloTan24})\).
\begin{equation}
-\tan(\alpha+\theta) = \frac{\frac{h}{m}+\frac{h}{n}}{\frac{h}{m}\cdot \frac{h}{n}-1}
\label{eq:AreaTrianguloTan27}
\end{equation}
\begin{equation}
-\tan(\alpha+\theta) = \frac{\frac{h(m+n)}{\cancel{mn}}}{\frac{h^2-mn}{\cancel{mn}}}
\label{eq:AreaTrianguloTan28}
\end{equation}
\begin{equation}
-\tan(\alpha+\theta) = \frac{h(m+n)}{h^2-mn}
\label{eq:AreaTrianguloTan30}
\end{equation}
Como \(m+n=c\) e \(h^2=b^2-m^2\), substituindo-os em (\(\ref{eq:AreaTrianguloTan30}\)),
\begin{equation}
-\tan(\alpha+\theta) = \frac{h\dot c}{b^2-m^2-mn}= \frac{h\dot c}{b^2-m(m+n)}
\label{eq:AreaTrianguloTan31}
\end{equation}
Como \(m+n=c\), substituindo-o em (\(\ref{eq:AreaTrianguloTan31}\)),
\begin{equation}
-\tan(\alpha+\theta) = \frac{h\dot c}{b^2-m\cdot c}
\label{eq:AreaTrianguloTan32}
\end{equation}
Substituindo \(m\) de (\(\ref{eq:AreaTrianguloTan17}\)) em (\(\ref{eq:AreaTrianguloTan32}\)),
\begin{equation}
-\tan(\alpha+\theta) = \frac{h\dot c}{b^2-\frac{(b^2+c^2-a^2)\cancel{c}}{2\cancel{c}}} = \frac{h\dot c}{\frac{2b^2- b^2-c^2+a^2}{2}}
\label{eq:AreaTrianguloTan33}
\end{equation}
\begin{equation}
-\tan(\alpha+\theta) = \frac{2h\dot c}{b^2+a^2-c^2}
\label{eq:AreaTrianguloTan34}
\end{equation}
Como a \(\tan(\beta)=-\tan(\alpha+\theta)\), logo,
\begin{equation}
\tan(\beta) = \frac{2h\dot c}{b^2+a^2-c^2}
\label{eq:AreaTrianguloTan35}
\end{equation}
Isolando \(h\),
\begin{equation}
h = \frac{b^2+a^2-c^2}{2c}\cdot \tan(\beta)
\label{eq:AreaTrianguloTan36}
\end{equation}
A área de um triângulo pode ser calculado pela fórmula abaixo,
\begin{equation}
A=\frac{base\cdot altura}{2}
\label{eq:AreaTrianguloTan37}
\end{equation}
Como a base do triângulo \(\triangle ABC\) é igual a \(c\) e a altura igual a \(h\), substituindo-os em (\(\ref{eq:AreaTrianguloTan37}\)),
\begin{equation}
A= \frac{\cancel{c}}{2} \cdot \frac{b^2+a^2-c^2}{2\cancel{c}}\cdot \tan(\beta)
\label{eq:AreaTrianguloTan38}
\end{equation}
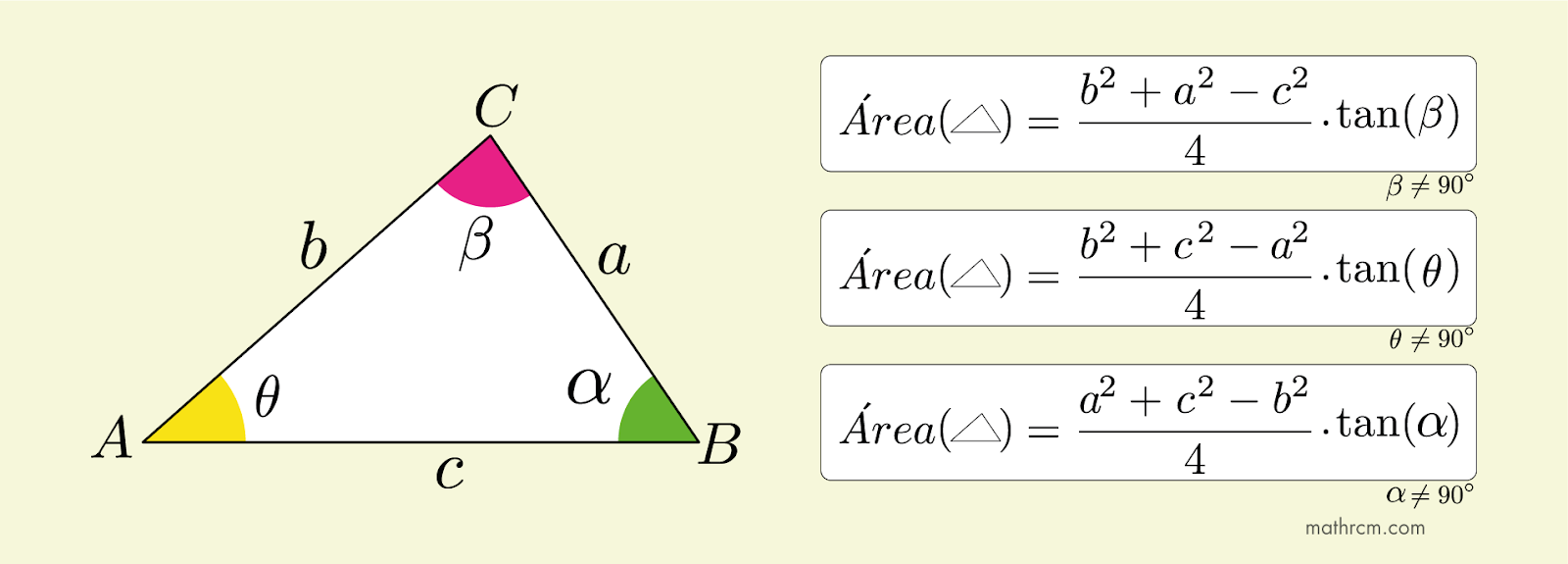
\begin{equation}
A= \frac{b^2+a^2-c^2}{4}\cdot \tan(\beta)
\label{eq:AreaTrianguloTan39}
\end{equation}
\(\blacksquare\)
Como a \(\tan(90\degree)\) não está definida, logo a fórmula acima não é válida para \(\beta = 90 \degree\). No entanto, podemos usar um dos outros dois ângulos. Portanto.
Notas e referências
Como fazer referência ao post
Rodrigo da Costa. Fórmula para calcular a área de um triângulo qualquer em função dos seus lados e da tangente de um ângulo conhecido. rcmath, 28/11/2023. Disponível em: < https://www.rcmath.com/2023/11/formula-para-calcular-a-area-de-um-triangulo-em-funcao-dos-seus-lados-e-da-tangente-de-um-angulo-conhecido.html >. Acesso em: .








0 comments:
Postar um comentário