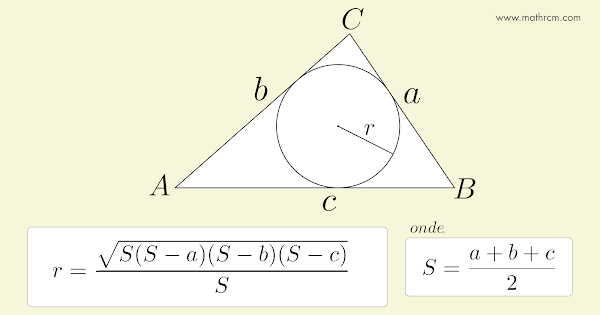
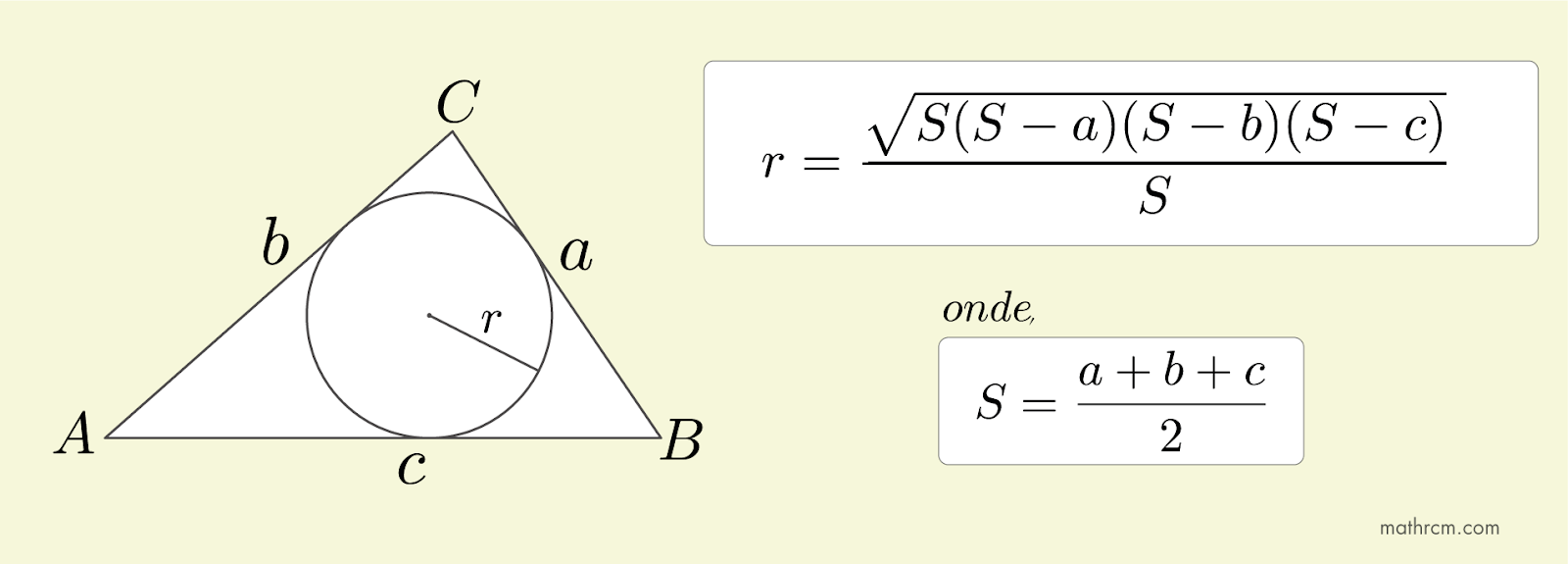
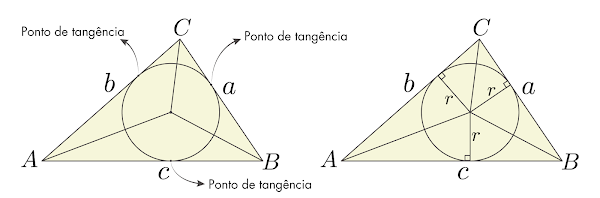
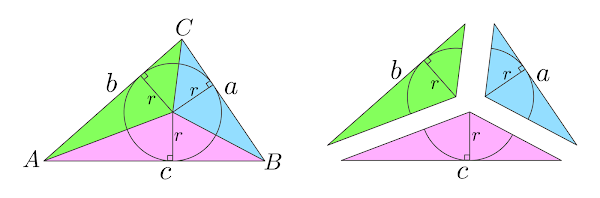
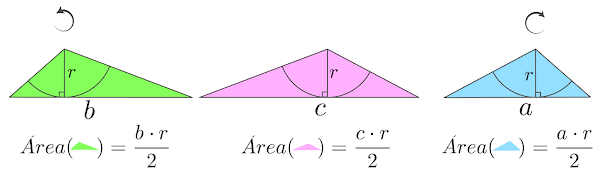
A altura de cada triângulo menor é o raio obtido ligando cada ponto de tangência, formados pela intersecção dos lados do triângulo com a circunferência, ao incentro. Cada triângulo menor tem como base um dos lados do triângulo maior \(\triangle ABC\) e altura igual ao raio \(r\) da circunferência inscrita, uma vez que o raio é perpendicular ao lado que tangencia a circunferência. A área de cada triângulo pode ser calculado pela fórmula \(Area=\frac{base\cdot altura}{2}\), logo. A soma das áreas dos três triângulos é igual a área do triângulo \(\triangle ABC\). Logo, a área do triângulo \(\triangle ABC\) é igual a, \begin{equation} A= \frac{b\cdot r}{2}+\frac{c\cdot r}{2}+\frac{a\cdot r}{2} \label{eq:AgulosDeTriagulo13} \end{equation} \begin{equation} A= \frac{(a+b+c)}{2}\cdot r \label{eq:Area14} \end{equation} Chamando, \begin{equation} S = \frac{a+b+c}{2} \label{eq:4.30} \end{equation} Logo, \begin{equation} A= S\cdot r \label{eq:Area15} \end{equation} A área em função dos lados do triângulo \(\triangle ABC\) pode ser calculada pela fórmula de Heron. \begin{equation} A =\sqrt{S(S-a)(S-b)(S-c)} \label{eq:4.29} \end{equation} Como \( (\ref{eq:Area15})\) e \( (\ref{eq:4.29})\) são iguais, logo. \begin{equation} S\cdot r = \sqrt{S(S-a)(S-b)(S-c)} \label{eq:Area16} \end{equation} Portanto, o comprimento do raio da circunferência inscrita em função dos lados do triângulo circunscrito é igual a. \begin{equation} r = \frac{\sqrt{S(S-a)(S-b)(S-c)}}{S} \label{eq:Area17} \end{equation} Em \( (\ref{eq:Area14})\) temos uma proporção interessante que relaciona a área, o perímetro do triângulo e o raio da circunferência inscrita. A área do triângulo está para o perímetro do triângulo, assim como o raio da circunferência inscrita está para \(2\). \begin{equation} \frac{A}{P} = \frac{r}{2} \label{eq:6.0.38} \end{equation}
\(\blacksquare\)
Uma outra forma de demonstrar o comprimento do raio da circunferência inscrita no triângulo é explorando um comportamento peculiar do incentro. A localização do incentro está localizada sobre a base do triângulo. Na figura abaixo, mantendo a base \(c\) fixa, podemos mover o ponto \(C\) para a esquerda, direita e para cima/baixo, o centro permanecerá na região azul. Sendo assim, o incentro sempre estará a direita do vértice \(A\) e a esquerda do vértice \(B\) não importando a localização do vértice \(C\).
Na Figura abaixo, chamando o comprimento a direita do vértice \(A\) de \(n\) e, \(m\) o comprimento a esquerda do vértice \(B\). Como o incentro é o ponto de encontro das três bissetrizes, logo o ângulo \(\angle PAO\) é metade do ângulo \(\angle BAC\) assim como, o ângulo \(\angle PBO\) é metade do ângulo \(\angle ABC\).
A \(\tan\left( \frac{\theta}{2}\right) \) no triângulo \(\triangle APO\) é igual a.
\begin{equation}
\tan\left( \frac{\theta}{2}\right) = \frac{r}{n}
\label{eq:6.0.2} %\tag{6.0.2}
\end{equation}
\begin{equation}
n = \frac{r}{\tan\left( \frac{\theta}{2}\right)}
\label{eq:6.0.3} %\tag{6.0.3}
\end{equation}
A \(\tan\left( \frac{\alpha}{2}\right) \) no triângulo \(\triangle BPO\) é igual a.
\begin{equation}
\tan\left( \frac{\alpha}{2}\right) = \frac{r}{m}
\label{eq:6.0.4} %\tag{6.0.4}
\end{equation}
\begin{equation}
m = \frac{r}{\tan\left( \frac{\alpha}{2}\right)}
\label{eq:6.0.5} %\tag{6.0.5}
\end{equation}
Somando (\ref{eq:6.0.3}) e (\ref{eq:6.0.5}).
\begin{equation}
n+m= \frac{r}{\tan\left( \frac{\theta}{2}\right)} + \frac{r}{\tan\left( \frac{\alpha}{2}\right)}
\label{eq:6.0.6} %\tag{6.0.6}
\end{equation}
Com \(n+m = c\), substituindo-o em (\ref{eq:6.0.6}).
\begin{equation}
c = \frac{r}{\tan\left( \frac{\theta}{2}\right)} + \frac{r}{\tan\left( \frac{\alpha}{2}\right)}
\label{eq:6.0.7} %\tag{6.0.7}
\end{equation}
\begin{equation}
c = \frac{r}{\tan\left( \frac{\theta}{2}\right)} + \frac{r}{\tan\left( \frac{\alpha}{2}\right)}
\label{eq:6.0.8} %\tag{6.0.8}
\end{equation}
\begin{equation}
c = r\cdot \left( \frac{\tan\left( \frac{\alpha}{2}\right) + \tan\left( \frac{\theta}{2}\right)}{\tan\left( \frac{\theta}{2}\right)\cdot\tan\left( \frac{\alpha}{2}\right)}\right)
\label{eq:6.0.9} %\tag{6.0.9}
\end{equation}
\begin{equation}
r = c\cdot \left( \frac{\tan\left( \frac{\theta}{2}\right)\cdot\tan\left( \frac{\alpha}{2}\right)}{\tan\left( \frac{\alpha}{2}\right) + \tan\left( \frac{\theta}{2}\right)}\right)
\label{eq:6.0.10} %\tag{6.0.10}
\end{equation}
Como conhecemos a identidade trigonometrica que relaciona a tangente da metade de um ângulo com o seno e o cosseno desse mesmo ângulo.
\begin{equation}
\tan\left( \frac{\theta}{2}\right) = \frac{\sin(\theta)}{1+(\cos\theta)}
\label{eq:6.0.11} %\tag{6.0.11}
\end{equation}
Assim como,
\begin{equation}
\tan\left( \frac{\alpha}{2}\right) = \frac{\sin(\alpha)}{1+\cos(\alpha)}
\label{eq:6.0.12} %\tag{6.0.12}
\end{equation}
Como já demonstramos as relações \(\sin\) e \(\cos\) para um triângulo qualquer.
\begin{equation}
\sin(\theta) = \sqrt{1-\left(\frac{b^2+c^2-a^2}{2bc}\right)^2} \label{eq:6.0.13} %\tag{6.0.13}
\end{equation}
\begin{equation}
\cos(\theta) = \frac{b^2+c^2-a^2}{2bc} \label{eq:6.0.14} %\tag{6.0.14}
\end{equation}
Assim como,
\begin{equation}
\sin(\alpha) = \sqrt{1-\left(\frac{a^2+c^2-b^2}{2ac}\right)^2} \label{eq:6.0.15} %\tag{6.0.15}
\end{equation}
\begin{equation}
\cos(\alpha) = \frac{a^2+c^2-b^2}{2ac} \label{eq:6.0.16} %\tag{6.0.16}
\end{equation}
Substituindo (\ref{eq:6.0.13}) e (\ref{eq:6.0.14}) em (\ref{eq:6.0.11}).
\begin{equation}
\tan\left( \frac{\theta}{2}\right) =\frac{\sqrt{1-\left(\frac{b^2+c^2-a^2}{2bc}\right)^2}}{1+\left( \frac{b^2+c^2-a^2}{2bc}\right) }
\label{eq:6.0.17} %\tag{6.0.17}
\end{equation}
\begin{equation}
\tan\left( \frac{\theta}{2}\right) = \frac{\frac{\sqrt{4b^2c^2-\left(b^2+c^2-a^2\right)^2}}{2bc}}{\frac{2bc+b^2+c^2-a^2}{2bc} }
\label{eq:6.0.18} %\tag{6.0.18}
\end{equation}
\begin{equation}
\tan\left( \frac{\theta}{2}\right) = \frac{\sqrt{4b^2c^2-\left(b^2+c^2-a^2\right)^2}}{2bc+b^2+c^2-a^2}
\label{eq:6.0.19} %\tag{6.0.19}
\end{equation}
\begin{equation}
\tan\left( \frac{\theta}{2}\right) = \frac{\sqrt{4b^2c^2-\left(b^2+c^2-a^2\right)^2}}{(a+b+c)(b+c-a)}
\label{eq:6.0.20} %\tag{6.0.20}
\end{equation}
\begin{equation}
\tan\left( \frac{\theta}{2}\right) = \frac{\sqrt{(a+b+c)(a+b-c)(a+c-b)(b+c-a)}}{(a+b+c)(b+c-a)}
\label{eq:6.0.21} %\tag{6.0.21}
\end{equation}
Analogamente, podemos repetir os passos acima para a \(\tan\left( \frac{\alpha}{2}\right)\).
\begin{equation}
\tan\left( \frac{\alpha}{2}\right) = \frac{\sqrt{4a^2c^2-\left(a^2+c^2-b^2\right)^2}}{(a+b+c)(b+c-b)}
\label{eq:6.0.22} %\tag{6.0.22}
\end{equation}
\begin{equation}
\tan\left( \frac{\alpha}{2}\right) = \frac{\sqrt{(a+b+c)(a+b-c)(a+c-b)(b+c-a)}}{(a+b+c)(a+c-b)}
\label{eq:6.0.23} %\tag{6.0.23}
\end{equation}
Substituindo (\ref{eq:6.0.21}) e (\ref{eq:6.0.23}) em (\ref{eq:6.0.10}).
\begin{equation}
r = c\cdot \left( \frac{\left( \frac{\sqrt{(a+b+c)(a+b-c)(a+c-b)(b+c-a)}}{(a+b+c)(b+c-a)} \right)\left( \frac{\sqrt{(a+b+c)(a+b-c)(a+c-b)(b+c-a)}}{(a+b+c)(a+c-b)} \right) }{ \left( \frac{\sqrt{(a+b+c)(a+b-c)(a+c-b)(b+c-a)}}{(a+b+c)(a+c-b)} \right) + \left( \frac{\sqrt{(a+b+c)(a+b-c)(a+c-b)(b+c-a)}}{(a+b+c)(b+c-a)} \right) } \right)
\label{eq:6.024} %\tag{6.0.24}
\end{equation}
\begin{equation}
r = c\cdot \left( \frac{\frac{\left(\sqrt{(a+b+c)(a+b-c)(a+c-b)(b+c-a)}\right) ^2}{(a+b+c)^2(b+c-a)(a+c-b)}}{\frac{\left( (a+c-b) +(b+c-a)\right) \sqrt{(a+b+c)(a+b-c)(a+c-b)(b+c-a)}}{(a+b+c)(b+c-a)(a+c-b)}}\right)
\label{eq:6.025} %\tag{6.0.25}
\end{equation}
\begin{equation}
r = c\cdot \left( \frac{\cancel{(a+b+c)}(a+b-c)\cancel{(a+c-b)}\cancel{(b+c-a)}}{\cancel{(a+b+c)^2}\cancel{(b+c-a)}\cancel{(a+c-b)}} \cdot \frac{\cancel{(a+b+c)}(b+c-a)(a+c-b)}{\left( 2c\right) \sqrt{(a+b+c)(a+b-c)(a+c-b)(b+c-a)}} \right)
\label{eq:6.026} %\tag{6.0.26}
\end{equation}
\begin{equation}
r = c\cdot \left(\frac{(a+b-c)(b+c-a)(a+c-b)}{\left(2c\right) \sqrt{(a+b+c)(a+b-c)(a+c-b)(b+c-a)}} \right)
\label{eq:6.027} %\tag{6.0.27}
\end{equation}
Racionalizando (\ref{eq:6.027}).
\begin{equation}
r = c\cdot \left(\frac{(a+b-c)(b+c-a)(a+c-b)\sqrt{(a+b+c)(a+b-c)(a+c-b)(b+c-a)}}{\left( 2c\right) \left( \sqrt{(a+b+c)(a+b-c)(a+c-b)(b+c-a)}\right)^2 } \right)
\label{eq:6.028} %\tag{6.0.28}
\end{equation}
\[
r = \cancel{c}\cdot \left(\frac{(a+b-c)(b+c-a)(a+c-b)\sqrt{(a+b+c)(a+b-c)(a+c-b)(b+c-a)}}{(2\cancel{c}) \left( \cancel{\vphantom{\sqrt{(a+b+c)(a+b-c)(a+c-b)(b+c-a)}}\hspace{1.5em}}\hspace{-1.5em}\sqrt{(a+b+c)(a+b-c)(a+c-b)(b+c-a)}\right)^{\cancel{2}} } \right)
\label{eq:6.029}
%\tag{6.0.29}
\]
\begin{equation}
r =\frac{\cancel{(a+b-c)}\cancel{(b+c-a)}\cancel{(a+c-b)}\sqrt{(a+b+c)(a+b-c)(a+c-b)(b+c-a)}}{2(a+b+c)\cancel{(a+b-c)}\cancel{(b+c-a)}\cancel{(a+c-b)}}
\label{eq:6.030}
\end{equation}
\begin{equation}
r =\frac{\sqrt{(a+b+c)(a+b-c)(a+c-b)(b+c-a)}}{2(a+b+c)}
\label{eq:6.031} %\tag{6.0.31}
\end{equation}
Multiplicando o numerador e o denominador a esquerda do sinal de igualdade de \((\ref{eq:6.031})\) por 2.
\begin{equation}
r =\frac{2\sqrt{(a+b+c)(a+b-c)(a+c-b)(b+c-a)}}{4(a+b+c)}
\label{eq:6.032}
\end{equation}
\begin{equation}
\frac{a+b+c}{2}\cdot r =\frac{\sqrt{(a+b+c)(a+b-c)(a+c-b)(b+c-a)}}{4}
\label{eq:6.033}
\end{equation}
Revertendo o numerador \(4\) para o radicando.
\begin{equation}
\frac{a+b+c}{2}\cdot r =\sqrt{\frac{(a+b+c)(a+b-c)(a+c-b)(b+c-a)}{16}}
\label{eq:6.034}
\end{equation}
Como \(16=2\cdot 2\cdot 2\cdot 2\).
\begin{equation}
\frac{a+b+c}{2}\cdot r =\sqrt{\frac{(a+b+c)}{2}.\frac{(a+b-c)}{2}.\frac{(a+c-b)}{2}.\frac{(b+c-a)}{2}}
\label{eq:4.22}
\end{equation}
Aplicando uma substituição simples,
\begin{equation}
S = \frac{a+b+c}{2}
\label{eq:4.23}
\end{equation}
Somando \(-c\) em ambos os lados de (\ref{eq:4.23}),
\begin{equation}
S - c= \frac{a+b+c}{2} -c
\label{eq:4.24}
\end{equation}
\begin{equation}
S - c= \frac{a+b+c-2c}{2}
\label{eq:4.25}
\end{equation}
\begin{equation}
S - c= \frac{a+b-c}{2}
\label{eq:4.26}
\end{equation}
Analogamente, podemos repetir os passos acima somando \(-a\) e \(-b\) para obtermos as outras duas relações.
\begin{equation}
S - b = \frac{a+c-b}{2}
\label{eq:4.27}
\end{equation}
\begin{equation}
S - a = \frac{b+c-a}{2}
\label{eq:4.28}
\end{equation}
Substituindo (\ref{eq:4.23}), (\ref{eq:4.26}), (\ref{eq:4.27}) e (\ref{eq:4.28}) na fórmula (\ref{eq:4.22}).
\begin{equation}
S\cdot r =\sqrt{S(S-a)(S-b)(S-c)}
\label{eq:4.269}
\end{equation}
\begin{equation}
r = \frac{\sqrt{S(S-a)(S-b)(S-c)}}{S}
\label{eq:4.350}
\end{equation}
Notas e referências
Como fazer referência ao post
Rodrigo da Costa. Demonstração do comprimento do raio da circunferência inscrita em um triângulo. rcmath, 26/11/2023. Disponível em: < https://www.rcmath.com/2023/11/demonstracao-do-comprimento-do-raio-da-circunferencia-inscrita-em-um-triangulo.html >. Acesso em: .









0 comments:
Postar um comentário