
Uma das formas de demonstrar a fórmula de Heron é a partir das
Leis dos Cossenos.
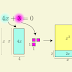
Aplicando a lei dos cossenos no triângulo \(\triangle ABC\), tendo como referência o ângulo \(\theta\) \(\measuredangle ABC\) .
 |
| Figura 1 |
\begin{equation}
a^2=b^2+c^2-2bc \cdot cos(\theta)
\label{eq:5.6}
\end{equation}
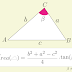
Traçando uma altura relativa a base \(c\), \(Figura (2)\), e aplicando Pitágoras ao triângulo \(\triangle APC\).
 |
| Figura 2 |
\begin{equation}
b^2=h^2+m^2
\label{eq:4.2}
\end{equation}
\begin{equation}
m^2=b^2-h^2
\label{eq:4.3}
\end{equation}
O cosseno do ângulo \(\theta\) \(\measuredangle APC\) do triângulo \(\triangle APC\) é igual a.
\begin{equation}
cos(\theta) = \frac{m}{b}
\label{eq:4.4}
\end{equation}
Substituindo (\ref{eq:4.4}) em (\ref{eq:5.6}) temos,
\begin{equation}
a^2=b^2+c^2-\frac{2\cancel{b}cm}{\cancel{b}}
\end{equation}
\begin{equation}
a^2=b^2+c^2-2cm
\label{eq:4.5}
\end{equation}
\begin{equation}
2cm=b^2+c^2-a^2
\label{eq:4.6}
\end{equation}
\begin{equation}
m=\frac{b^2+c^2-a^2}{2c}
\label{eq:4.7}
\end{equation}
Elevando os dois lados da igualdade (\ref{eq:4.7}) ao quadrado.
\begin{equation}
m^{2}=\frac{(b^2+c^2-a^2)^{2}}{4c^{2}}
\label{eq:4.8}
\end{equation}
Substituindo (\ref{eq:4.3}) em (\ref{eq:4.8}) temos,
\begin{equation}
b^{2}-h^{2}=\frac{(b^2+c^2-a^2)^{2}}{4c^{2}}
\label{eq:4.9}
\end{equation}
\begin{equation}
h^{2}=b^{2}-\frac{(b^2+c^2-a^2)^{2}}{4c^{2}}
\label{eq:4.10}
\end{equation}
\begin{equation}
h^{2}=\frac{4b^{2}c^{2}-(b^2+c^2-a^2)^{2}}{4c^{2}}
\label{eq:4.11}
\end{equation}
Portanto, a altura de qualquer triângulo em função dos segmentos é dada pela fórmula abaixo.
\begin{equation}
h=\frac{\sqrt{4b^{2}c^{2}-(b^2+c^2-a^2)^{2}}}{2c}
\label{eq:4.12}
\end{equation}
Como a área de um triângulo é dada pela fórmula abaixo,
\begin{equation}
A=\frac{base \cdot altura}{2}
\label{eq:4.13}
\end{equation}
Substituindo em (\ref{eq:4.13}) a base que é igual a \(c\), e a altura que é dada pela fórmula (\ref{eq:4.12}), temos.
\begin{equation}
A =\frac{\cancel{c}\sqrt{4b^{2}c^{2}-(b^2+c^2-a^2)^{2}}}{2.\cancel{c}.2}
\label{eq:4.14}
\end{equation}
Portanto, a área de um triângulo qualquer em função dos seus segmentos é dada pela fórmula abaixo.
\begin{equation}
A =\frac{\sqrt{4b^{2}c^{2}-(b^2+c^2-a^2)^{2}}}{4}
\label{eq:4.15}
\end{equation}
Com algumas manipulações algébricas chegaremos à fórmula de
Heron. Como a parte interna do radical (lê-se radicando) em (\ref{eq:4.15}) é uma diferença de quadrados.
\begin{equation}
A =\frac{\sqrt{(2bc)^{2}-(b^2+c^2-a^2)^{2}}}{4}
\label{eq:4.16}
\end{equation}
\begin{equation}
A =\frac{\sqrt{(2bc-b^2-c^2+a^2)(2bc+b^2+c^2-a^2)}}{4}
\label{eq:4.17}
\end{equation}
\begin{equation}
A =\frac{\sqrt{(a^2-(b^2-2bc+c^2))((b^2+2bc+c^2)-a^2)}}{4}
\label{eq:4.18}
\end{equation}
\begin{equation}
A =\frac{\sqrt{(a^2-(b-c)^2)((b+c)^2-a^2)}}{4}
\label{eq:4.19}
\end{equation}
\begin{equation}
A =\frac{\sqrt{(a+c-b)(a+b-c)((b+c-a)(a+b+c))}}{4}
\label{eq:4.20}
\end{equation}
Fazendo a reversão do denominador para o radicando.
\begin{equation}
A =\sqrt{\frac{(a+c-b)(a+b-c)(b+c-a)(a+b+c)}{16}}
\label{eq:4.21}
\end{equation}
Como \(16=2\cdot2\cdot2\cdot2\) logo,
\begin{equation}
A =\sqrt{\frac{(a+b+c)}{2}.\frac{(a+b-c)}{2}.\frac{(a+c-b)}{2}.\frac{(b+c-a)}{2}}
\label{eq:4.22}
\end{equation}
Aplicando uma substituição simples,
\begin{equation}
S = \frac{a+b+c}{2}
\label{eq:4.23}
\end{equation}
Somando \(-c\) em ambos os lados de (\ref{eq:4.23}),
\begin{equation}
S - c= \frac{a+b+c}{2} -c
\label{eq:4.24}
\end{equation}
\begin{equation}
S - c= \frac{a+b+c-2c}{2}
\label{eq:4.25}
\end{equation}
\begin{equation}
S - c= \frac{a+b-c}{2}
\label{eq:4.26}
\end{equation}
Analogamente, podemos repetir os passos acima somando \(-a\) e \(-b\) para obtermos as outras duas relações.
\begin{equation}
S - b = \frac{a+c-b}{2}
\label{eq:4.27}
\end{equation}
\begin{equation}
S - a = \frac{b+c-a}{2}
\label{eq:4.28}
\end{equation}
Substituindo (\ref{eq:4.23}), (\ref{eq:4.26}), (\ref{eq:4.27}) e (\ref{eq:4.28}) na fórmula (\ref{eq:4.22}).
\begin{equation}
A =\sqrt{S(S-a)(S-b)(S-c)}
\label{eq:4.29}
\end{equation}
Onde,
\begin{equation}
S = \frac{a+b+c}{2}
\label{eq:4.30}
\end{equation}
Notas e referências
Como fazer referência ao post
Rodrigo da Costa. Demonstração da Fórmula de Heron a partir da Lei dos Cossenos. rcmath, 13/11/2023. Disponível em: < https://www.rcmath.com/2023/11/demonstracao-da-formula-de-heron-a-partir-da-lei-dos-cossenos.html >. Acesso em: .








0 comments:
Postar um comentário