\(\blacksquare\)
"Heronificando" lê-se - Deixar com a aparência da fórmula de Heron.
Dividido o numerador e o denominador por 8.
\begin{equation}
A = \frac{\frac{\pi (a+b-c)(a+c-b)(b+c-a)}{8}}{\frac{4(a+b+c)}{8}} \label{eq:6.2.4} %\tag{6.2.3}
\end{equation}
\begin{equation}
A = \frac{\pi \frac{(a+b-c)}{2} \cdot \frac{(a+c-b)}{2} \cdot \frac{(b+c-a)}{2}}{\frac{(a+b+c)}{2}} \label{eq:6.2.5} %\tag{6.2.3}
\end{equation}
Chamando \(S=\frac{(a+b+c)}{2}\).
\begin{equation}
A = \frac{\pi (S-a)(S-b)(S-a)}{S} \label{eq:6.2.6} %\tag{6.2.3}
\end{equation}
O perímetro pode ser calculado por.
\begin{equation}
P = 2\pi r \label{eq:6.3} %\tag{6.3}
\end{equation}
\begin{equation}
P = \cancel{2}\pi\frac{\sqrt{(a+b+c)(a+b-c)(a+c-b)(b+c-a)}}{\cancel{2}(a+b+c)} \label{eq:6.3.1} %\tag{6.3.1}
\end{equation}
\begin{equation}
P = \pi\frac{\sqrt{(a+b+c)(a+b-c)(a+c-b)(b+c-a)}}{(a+b+c)} \label{eq:6.3.2} %\tag{6.3.2}
\end{equation}
Dividindo o numerador e o denominador por 4.
\begin{equation}
P = \frac{\frac{\pi\sqrt{(a+b+c)(a+b-c)(a+c-b)(b+c-a)}}{4}}{\frac{(a+b+c)}{4}} \label{eq:6.3.3} %\tag{6.3.2}
\end{equation}
Revertendo \(4\) para o radicando.
\begin{equation}
P = \frac{\pi\sqrt{\frac{(a+b+c)}{2}\frac{(a+b-c)}{2}\frac{(a+c-b)}{2}\frac{(b+c-a)}{2}}}{\frac{1}{2}\cdot\frac{a+b+c}{2}} \label{eq:6.3.4} %\tag{6.3.2}
\end{equation}
Chamando \(S=\frac{(a+b+c)}{2}\).
\begin{equation}
P = \frac{\pi\sqrt{S(S-a)(S-b)(S-c)}}{\frac{S}{2}} \label{eq:6.3.5} %\tag{6.3.2}
\end{equation}
Portanto, o perímetro, em função dos lados do triângulo, é dado por.
\begin{equation}
P = \frac{2\pi\sqrt{S(S-a)(S-b)(S-c)}}{S} \label{eq:6.3.6} %\tag{6.3.2}
\end{equation}
Notas e referências
Como fazer referência ao post
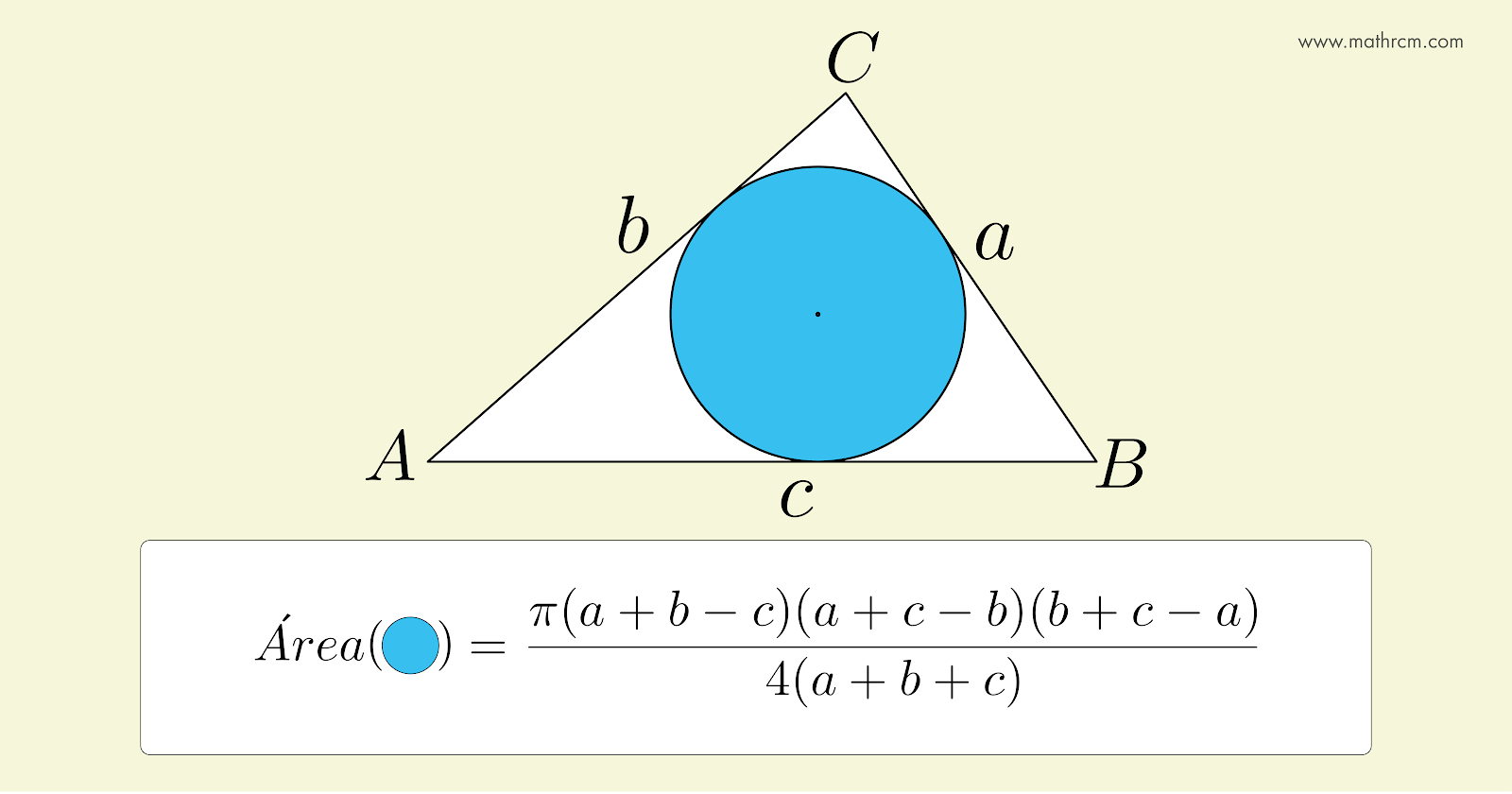
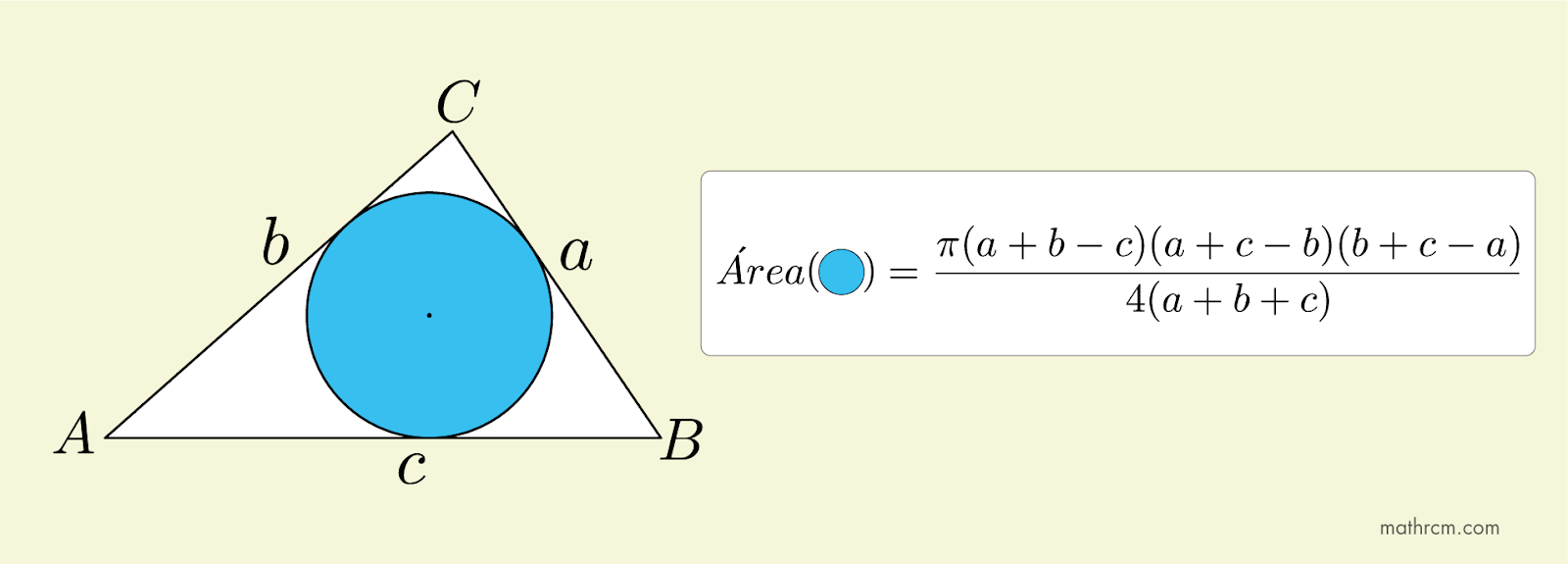
Rodrigo da Costa. A área do círculo em função dos lados de um triângulo circunscrito. rcmath, 28/11/2023. Disponível em: < https://www.rcmath.com/2023/11/a-area-do-circulo-em-funcao-dos-lados-do-triangulo-circunscrito.html >. Acesso em: .





0 comments:
Postar um comentário