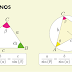
A bissetriz interna de um triângulo é o segmento de reta que inicia-se em um dos vértices e prolonga-se até o lado oposto, dividido o ângulo do ponto de partida em duas partes iguais.
 |
| Figura 1 |
\(\require{gensymb}\)
O teorema da bissetriz interna.
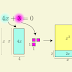
A partir do vértice \(B\) cria-se um segmento \(t\) paralelo a \(g\) e prologa o segmento \(b\) até coincidir com o segmento \(t\), no ponto \(P\).
 |
| Figura 2 |
Como \(g \| t\), o ângulo \(\measuredangle BPC\) e \(\beta\) são alternos interno .
 |
| Figura 3 |
A soma dos ângulos interno de um triângulo é igual a \(180 \degree\), sendo assim, no triângulo \(\triangle BCP\).
\begin{equation}
\beta + (180\degree - 2\beta) + \gamma = 180\degree
\label{eq:TeoremaBissetriz1}
\end{equation}
\begin{equation}
\beta + \cancel{180\degree} - 2\beta + \gamma = \cancel{180\degree}
\label{eq:TeoremaBissetriz2}
\end{equation}
\begin{equation}
- \beta + \gamma = 0
\label{eq:TeoremaBissetriz3}
\end{equation}
\begin{equation}
\gamma = \beta
\label{eq:TeoremaBissetriz4}
\end{equation}
Como \(\gamma = \beta\), o triângulo \(\triangle BCP\) é isósceles. Sendo assim o segmento \(\overline{\rm CP} = a\).
 |
| Figura 4 |
Pelo
Teorema de interceptação (usualmente chamado de "O teorema de Tales"), obtemos a seguinte relação.
 |
| Figura 5 |
O segmento \(a\) está para \(b+a\), assim como \(m\) está para \(n+m = c\).
\begin{equation}
\frac{a}{b+a} = \frac{m}{c}
\label{eq:TeoremaBissetriz5}
\end{equation}
\begin{equation}
m = \frac{ac}{a+b}
\label{eq:TeoremaBissetriz6}
\end{equation}
O segmento \(b\) está para \(b+a\), assim como \(n\) está para \(n+m=c\).
\begin{equation}
n = \frac{bc}{a+b}
\label{eq:TeoremaBissetriz7}
\end{equation}
Como conhecemos \(n\) e \(m\), podemos obter o comprimento da bissetriz \(g\).
 |
| Figura 6 |
O teorema da bissetriz interna diz que, o segmento \(b\) está para \(n\), na mesma razão que \(a\) está para \(m\).
\begin{equation}
\frac{b}{n} = \frac{a}{m}
\label{eq:TeoremaBissetriz7.1}
\end{equation}
Demonstração do comprimento da bissetriz interna.
O \(\cos(\beta)\), obtido pela lei dos cossenos, no triângulo \(\triangle CAQ\) é igual a.
 |
| Figura 7 |
\begin{equation}
\cos(\beta) = \frac{b^2+g^2-n^2}{2gb}
\label{eq:TeoremaBissetriz8}
\end{equation}
O \(\cos(\beta)\), obtido pela
lei dos Cossenos, no triângulo \(\triangle CBQ\) é igual a.
 |
| Figura 8 |
\begin{equation}
\cos(\beta) = \frac{a^2+g^2-m^2}{2ab}
\label{eq:TeoremaBissetriz9}
\end{equation}
Como o \(\cos(\beta)\) em ambos os triângulos \(\triangle CAQ\) e \(\triangle CBQ\) são iguais.
\begin{equation}
\cos(\beta) = \frac{b^2+g^2-n^2}{2gb}= \frac{a^2+g^2-m^2}{2ab}
\label{eq:TeoremaBissetriz10}
\end{equation}
\begin{equation}
\frac{b^2+g^2-n^2}{\cancel{2g}b}= \frac{a^2+g^2-m^2}{\cancel{2g}a}
\label{eq:TeoremaBissetriz11}
\end{equation}
\begin{equation}
a(b^2+g^2-n^2)= b(a^2+g^2-m^2)
\label{eq:TeoremaBissetriz12}
\end{equation}
Como conhecemos \(m\) e \(n\), substituindo-os em (\(\ref{eq:TeoremaBissetriz12}\)).
\begin{equation}
a\left( b^2+g^2-\left( \frac{bc}{a+b}\right)^2\right) = b\left( a^2+g^2-\left( \frac{ac}{a+b}\right) ^2\right)
\label{eq:TeoremaBissetriz13}
\end{equation}
\begin{equation}
ab^2+ag^2-\frac{ab^2c^2}{(a+b)^2} = ba^2+bg^2-\frac{ba^2c^2}{(a+b)^2}
\label{eq:TeoremaBissetriz14}
\end{equation}
\begin{equation}
ag^2-bg^2 = ba^2-\frac{ba^2c^2}{(a+b)^2} -ab^2 - \frac{ab^2c^2}{(a+b)^2}
\label{eq:TeoremaBissetriz15}
\end{equation}
\begin{equation}
g^2(a-b) = \frac{ba^2(a+b)^2-ba^2c^2 -ab^2(a+b)^2 + ab^2c^2}{(a+b)^2}
\label{eq:TeoremaBissetriz16}
\end{equation}
\begin{equation}
g^2 = \frac{ba^2(a+b)^2-ba^2c^2 -ab^2(a+b)^2 + ab^2c^2}{(a-b)(a+b)^2}
\label{eq:TeoremaBissetriz17}
\end{equation}
\begin{equation}
g^2 = \frac{(a+b)^2(ba^2 -ab^2)+c^2(ab^2-ba^2)}{(a-b)(a+b)^2}
\label{eq:TeoremaBissetriz18}
\end{equation}
\begin{equation}
g^2 = \frac{(a+b)^2(ba^2 -ab^2)-c^2(ba^2-ab^2)}{(a-b)(a+b)^2}
\label{eq:TeoremaBissetriz19}
\end{equation}
\begin{equation}
g^2 = \frac{(ba^2 -ab^2)((a+b)^2-c^2)}{(a-b)(a+b)^2}
\label{eq:TeoremaBissetriz20}
\end{equation}
\begin{equation}
g^2 = \frac{ab\cancel{(a-b)}((a+b)^2-c^2)}{\cancel{(a-b)}(a+b)^2}
\label{eq:TeoremaBissetriz21}
\end{equation}
\begin{equation}
g^2 = \frac{ab((a+b)^2-c^2)}{(a+b)^2}
\label{eq:TeoremaBissetriz22}
\end{equation}
\begin{equation}
g^2 = ab\left( \frac{(a+b)^2}{(a+b)^2} - \frac{c^2}{(a+b)^2}\right)
\label{eq:TeoremaBissetriz23}
\end{equation}
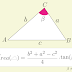
Portanto, o comprimento da bissetriz interna \(g\) é dado pela fórmula abaixo.
\begin{equation}
g = \sqrt{ab\left( 1 - \frac{c^2}{(a+b)^2}\right)}
\label{eq:TeoremaBissetriz24}
\end{equation}
Analogamente, podemos repetir os passos acima, tendo como referência os demais ângulos \(\alpha\) e \(\theta\), para obtermos os comprimentos das bissetrizes \(g_{2}\) e \(g_{3}\).
\begin{equation}
g_{2}=\sqrt{ac\left( 1-\frac{b^2}{(a+c)^2} \right) }
\label{eq:bissetriz0.2}
\end{equation}
\begin{equation}
g_{3}=\sqrt{bc\left( 1-\frac{a^2}{(b+c)^2} \right) }
\label{eq:bissetriz0.3}
\end{equation}
Notas e referências