O método de completar quadrados consiste em manipular cada termo de uma equação quadrática como sendo a área de um retângulo, adicionando ou removendo termos até completar um quadrado a esquerda do sinal de igualdade. Começaremos resolvendo dois exemplos antes de partir para a generalização do metódo, ou seja, definir uma fórmula para resolver qualquer equação.
Exemplo 1:
\begin{equation}
x^2+2x+1=0
\label{eq:completarQua1}
\end{equation}
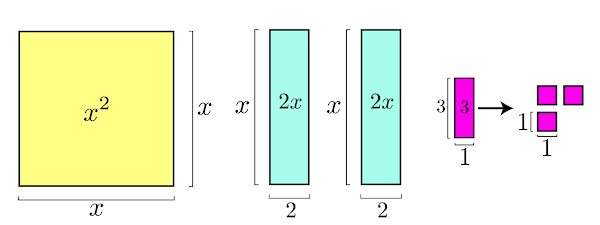
Definindo cada termo a esquerda do sinal de igualdade da equação acima como sendo a área de um retângulo.
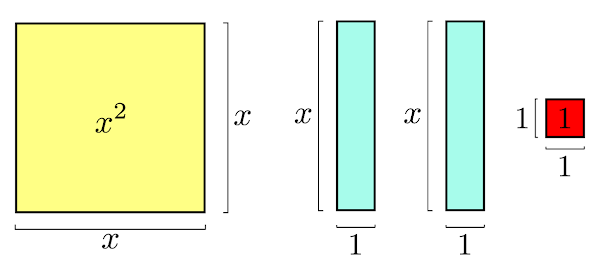
O termo \(x^2 \) pode ser interpretado como sendo a área de um quadrado de lado \(x\). O termo \(2x\) a área de um retângulo, cuja base é igual a \(2\) e altura \(x\), já o número \(1\) é a área de um quadrado unitário.
O nosso objetivo é transformar todo o lado esquerdo da equação em um único quadrado, para tanto, fatiaremos o retângulo de área \(2x\) para agrupa-lo no quadrado de área \(x^2\), horizontalmente e verticalmente.
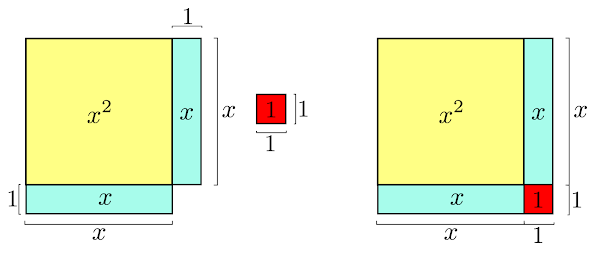
Dividindo ao meio o retângulo de área \(2x\) garantiremos que o quadrado amarelo aumente a sua área, tanto horizontalmente quanto verticalmente, na mesma proporção. Note que quando agrupamos os retângulos azuis no quadrado amarelo falta exatamente uma unidade de área, sendo assim, basta completar o espaço que falta com o quadrado unitário vermelho.
A equação é um quadrado perfeito a esquerda do sinal de igualdade, mas claro, nem sempre isso vai acontecer. As vezes é necessário adicionar/remover área para completar o quadrado.
A área do quadrado verde, de lado medindo \(x+1\), é a soma das áreas \(x^2\), \(2x\) e \(1\).
\begin{equation}
x^2+2x+1=(x+1)^2
\label{eq:completarQua2}
\end{equation}
Portanto, a equação (\(\ref{eq:completarQua1}\)) pode ser rescrita como,
\begin{equation}
(x+1)^2=0
\label{eq:completarQua3}
\end{equation}
A solução para \(x\) é \(-1\).
Exemplo 2:
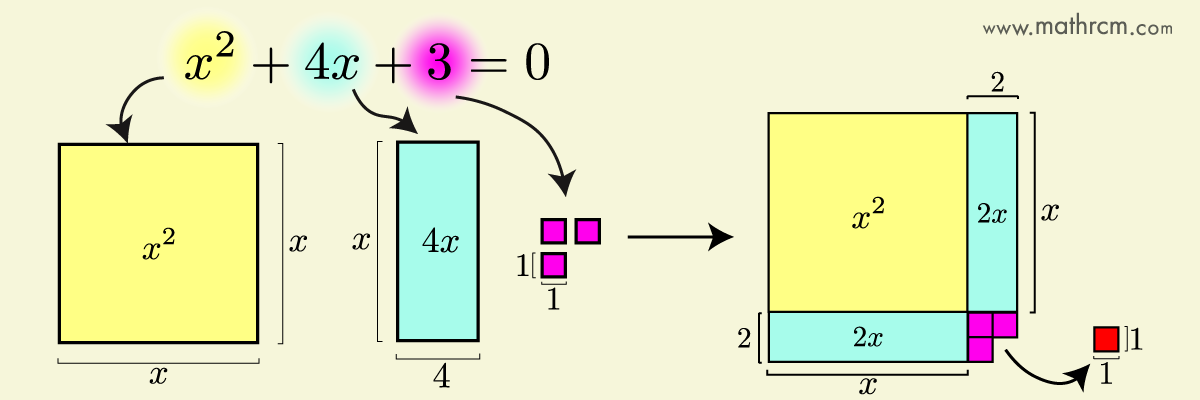
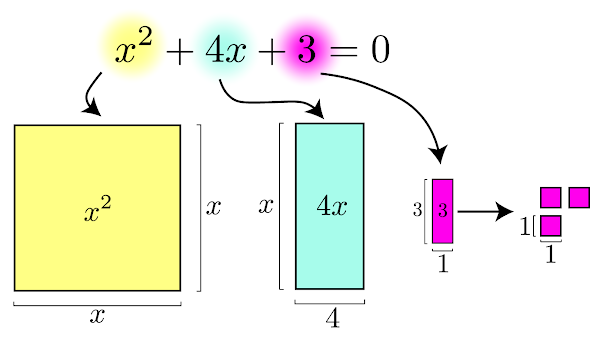
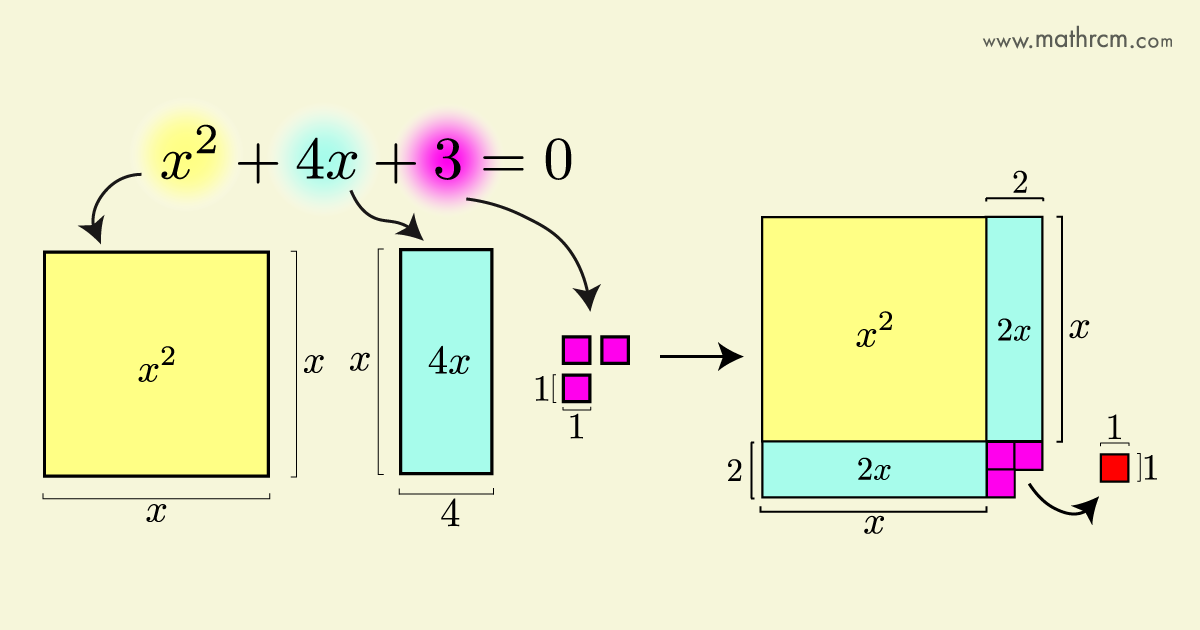
No próximo exemplo, para completar o quadrado será necessário adicionar mais área na equação.
\begin{equation}
x^2+4x+3=0
\label{eq:completarQua4}
\end{equation}
Dividido ao meio o retângulo de área \(4x\).
Não foi possível fazer um quadrado perfeito, pois faltou uma unidade de área.
Como podemos adicionar valores em ambos os lados da igualdade, adicionando \(+1\), tem-se.
\begin{equation}
x^2+4x+3+1=1
\label{eq:completarQua5}
\end{equation}
\begin{equation}
x^2+4x+4=1
\label{eq:completarQua6}
\end{equation}
O lado esquerdo da equação (\(\ref{eq:completarQua6}\)) é um quadrado perfeito, logo.
\begin{equation}
x^2+4x+4=(x+2)^2=1
\label{eq:completarQua7}
\end{equation}
Resolvendo, extraindo a raiz quadrada em ambos lados de (\(\ref{eq:completarQua7}\) ),
\begin{equation}
x+2=\pm 1
\label{eq:completarQua8}
\end{equation}
\begin{equation}
x=\pm 1 -2
\label{eq:completarQua9}
\end{equation}
\begin{equation}
x=\left\lbrace -3, -1 \right\rbrace
\label{eq:completarQua10}
\end{equation}
Generalização do método para obter a fórmula quadrática
Seja a equação quadrática abaixo com coeficientes \(a\), \(b\) e \(c\). Com \(a \neq 0\).
\begin{equation}
ax^2+bx+c=0
\label{eq:completarQua11}
\end{equation}
Dividindo cada termo da equação pelo coeficiente \(a\).
\begin{equation}
x^2+\frac{b}{a}x+\frac{c}{a}=0
\label{eq:completarQua12}
\end{equation}
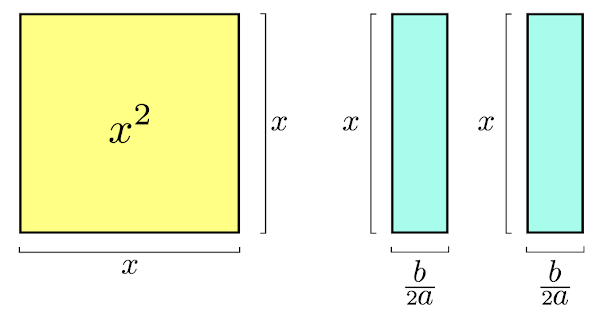
Manipularemos os termos que contém a variável \(x\) uma vez que não temos mais informações sobre o termo \(\frac{c}{a}\).
Dividindo ao meio o retângulo azul de área \(\frac{b}{a}x\).
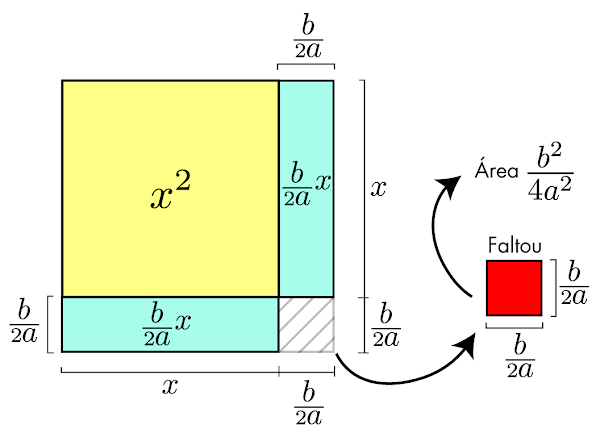
Acoplando, horizontalmente e verticalmente, as fatias do retângulo azul no quadrado amarelo.
Note que faltou um quadrado, cuja área é conhecida, mas não usaremos a área disponível \(\frac{c}{a}\) da equação, uma vez que não temos mais informações sobre esse termo. Como podemos adicionar ou remover termos sem alterar a equação, basta completar o quadrado adicionando em ambos os lados da equação a área que está faltando.
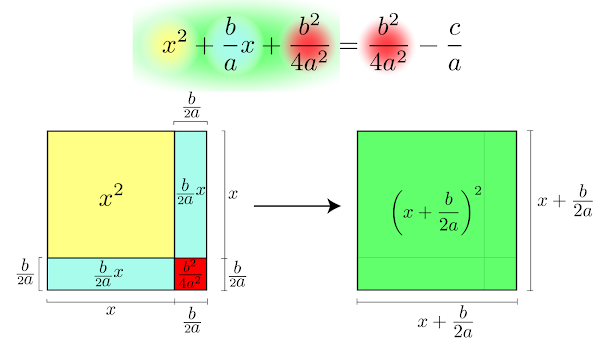
Deixando apenas os termos que corresponde a área do quadrado verde à esquerda do sinal de igualdade, para tanto, basta "passar" o termo \(\frac{c}{a}\) para o lado direito do sinal de igualdade.
\begin{equation}
\left( x+\frac{b}{2a} \right) ^2=\frac{b^2}{4a^2}-\frac{c}{a}
\label{eq:completarQua13}
\end{equation}
\begin{equation}
\left( x+\frac{b}{2a} \right)^2=\frac{b^2-4ac}{4a^2}
\label{eq:completarQua14}
\end{equation}
Extraindo a raiz quadrada em ambos os lados da equação (\(\ref{eq:completarQua14}\)).
\[
\cancel{\vphantom{\sqrt{\left( x+\frac{b}{2a} \right) ^{\cancel{2}}}}\hspace{1.5em}}\hspace{-1.5em}\sqrt{\left( x+\frac{b}{2a} \right)^{\cancel{2}}}= \sqrt{\frac{b^2-4ac}{4a^2}}
\label{eq:6.029}
\tag{14.1}
\]
\begin{equation}
x+\frac{b}{2a}=\pm \frac{\sqrt{b^2-4ac}}{2a}
\label{eq:completarQua15}
\end{equation}
\begin{equation}
x=-\frac{b}{2a}\pm \frac{\sqrt{b^2-4ac}}{2a}
\label{eq:completarQua16}
\end{equation}
Portanto, os valores de \(x\) da equação acima podem ser calculados pela fórmula quadrática (usualmente chamada de fórmula de Bhaskara).
\begin{equation}
x=\frac{-b \pm \sqrt{b^2-4ac}}{2a}
\label{eq:completarQua17}
\end{equation}
\(\blacksquare\)
Desafio 1:
Resolva a equação abaixo pelo método de completar quadrado.
\begin{equation}
x^2-6x+4=0
\label{eq:completarQua18}
\end{equation}
Solução:
Clique aqui
Podemos obter informações importantes sobre o \(\Delta\), lê-se Delta, da equação apenas observado se faltou/sobrou ou não área para completar o quadrado.
- Se faltou área para completar o quadrado, então, o valor de \(\Delta > 0\).
- Caso não sobre ou falte área para completar o quadrado, então, \(\Delta = 0\).
- Se sobrou área para completar o quadrado, então, o valor de \(\Delta < 0\).
Discutiremos mais sobre o assunto em uma próxima postagem.